huskydc
- 78
- 0
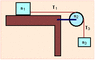
A block of mass m1 = 1 kg rests on a table with which it has a coefficient of friction µ = 0.77. A string attached to the block passes over a pulley to a block of mass m3 = 3 kg. The pulley is a uniform disk of mass m2 = 0.7 kg and radius 15 cm. As the mass m3 falls, the string does not slip on the pulley.
With what acceleration does the mass m3 fall?
i did the following:
[A]sum of Force on mass 1: T(1) - f = m(1) a
thus, T(1) = m(1)a + mu*m(1)g
sum of torque on mass 2: RT(3) = I *alpha
[C]sum of forces on mass 3: m(3)a = m(3)g - T(3)
thus, T(3) = m(3)g - m(3)a
and since alpha = a/R and I = .5 m(2) R^2
I plug in equatiion for T(3) into , and got something like this:
R m(3) g
------------------- =a
.5 m(2) R + R m(3)
and plug in numbers, didn't work out...any hints?
With what acceleration does the mass m3 fall?
i did the following:
[A]sum of Force on mass 1: T(1) - f = m(1) a
thus, T(1) = m(1)a + mu*m(1)g
sum of torque on mass 2: RT(3) = I *alpha
[C]sum of forces on mass 3: m(3)a = m(3)g - T(3)
thus, T(3) = m(3)g - m(3)a
and since alpha = a/R and I = .5 m(2) R^2
I plug in equatiion for T(3) into , and got something like this:
R m(3) g
------------------- =a
.5 m(2) R + R m(3)
and plug in numbers, didn't work out...any hints?