aaronfue
- 118
- 0
Homework Statement
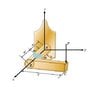
A locked door handle is composed of a solid circular shaft AB with a diameter of b = 108mm and a flat plate BC with a force P = 69N applied at point C as shown. Let c = 532mm , d = 126mm , and e = 153mm .
Homework Equations
\taumax = \frac{Tc}{J}
T = internal torque acting at cross section
c = outer radius
J = polar moment of inertia → J = \frac{\pi}{2}c4
The Attempt at a Solution
I've converted all mm to m.
I just wanted to see if someone could verify that I am on the right track.
radius, c = 0.054 m
1. The torque caused by the P force:
69 N × 0.532 m = 36.71 N*m → acting along the length of the solid shaft.
2. Internal torque, T:
T = 36.71 N*m *0. 126 m = 4.62546 N*m → acting at section m-m
3. J = \frac{\pi}{2}0.054 m4 = 13.36×10-6m4
\taumax = \frac{(4.62546 N*m)*(0.054 m)}{13.36×10^{-6} m^4}