jesstryin
- 8
- 0
Homework Statement
Calculate the net force acting on each object indicated in the diagrams. Show your work.
Homework Equations
a2 = b2 + c2
tanO = opposite/adjacent
C2 = a2 + b2 – 2abCosC
sina/A=sinb/B=sinc/C
The Attempt at a Solution
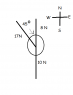
I attached the diagram below, it is the same as in my learning materials but I cannot share the actual course files so I recreated it just to show where the numbers are.
I am asked to find the net force acting on the object, here are my calculations:
a2 = 102 + 82
a = 12.8 N
tanO = opposite/adjacent
tanO = 10/8
51.34 or 51⁰
180 – (51 + 45)
84
C2 = a2 + b2 – 2abCosC
C = [ (a)2 + (b)2 – 2abCosC]1/2
C = [(12.8)2 + (17)2 – 2(12.8) * (17)cos84)]1/2
C =20.18
sina/A=sinb/B=sinc/C
sinb/17=sin84/20.18
=56.9
51⁰ - 56.9 = -5.9
I am confused because my result is negative. If it is not correct, can someone show me where to plug the numbers in for the equations, and if I am using the appropriate numbers? In the first equation, should I be using 10N and 17N instead, or are the numbers I have in the correct place?
Please let me know where the numbers are input for the equations to be done correctly. I would appreciate the help in laymen's terms, I understand everyone here is smart but I am not well versed in the language of physics yet.
Thanks for helping if you do :)