Mechaman
- 37
- 1
Homework Statement
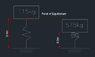
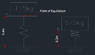
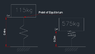
A mass of 115kg is to be suspended from a spring. When the mass increases to 575kg, the spring will move. Find the spring constant k. (This is not from a textbook, it is a project problem for a vehicle unloaded and then loaded on the same spring).
y1 is the maximum height I have but y2 can be changed if needed.
Homework Equations
(y1-y2)k = mg
The Attempt at a Solution
(0.2)k = (575)(9.81)
k = 5,640/0.2
k = 28,200N/m
This looks very wrong, comparing to a website that sells a spring holding 1300lb (590kg) gives a rate of 300(136kg/m) or around 1,300N/m
How is my answer so wrong?
Attachments
Last edited: