Adel Makram
- 632
- 15
Homework Statement
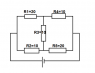
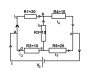
How to calculate the value of total resistance RT in the shown circuit?
Homework Equations
The Attempt at a Solution
I used Kirchhoff` first law: i1+i2=I where i1, i2 and I are the current passing through R1, R2 and the total current in the circuit, respectively.
similarly, i4+i5=I,
i1+i3=i4
i3+i5=i2
Then I used Kirchhoff` second law,
20 i1+10 i4=V0
10 i2+20 i5=V0.