bobred
- 170
- 0
Homework Statement
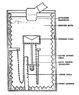
There is a submerged float which is held in equilibrium by three hanging chains (see attached), a portion of the chain hangs below the float. Ultrasound directed onto the top face of the float (which is concave with angle α) and the float is displaced downward proportional to the ultrasound power. Find the power as a function of displacement.
Homework Equations
Power W=\frac{Fc}{2\cos^2\alpha}
Where F is the force and c is the speed of sound in water
The Attempt at a Solution
I need to relate the distance of the float displacement to the Force.
As it is displaced the weight of the chain decreases. Linear density is mass over length, I know the length of the chains and their masses, all the same.
How do I work out the loss of weight?