How to calculate vector angles and magnitude

[jamesjames365]

Ok I am a little stuck and really need some help as I am pretty new with physics...im not sure if this question is really simple or if i need a little algebra to help find the answer.

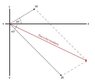
Q : 10 units, 30 degrees counterclockwise from the positive side of the x-axis
:25 units, 45 degrees clockwise from the negative side of the x-axis
Find the resultant magnitude and the angle of the two vectors.

Does this make sense?

Any help or advice would be great, thanks.

 

[Delphi51]

Separate each vector into its x and y components; 10*cos(30) and 10*sin(30) for the first one. Add the components. Then sketch the components and find the combined vector magnitude using the pythagorean theorem and the angle using trigonometry.

 

[jamesjames365]

wow thanks delphi51 but youre talking to someone who doesn't actually have a scientific calculator or knows how to do what you mention...thanks for the advice though, ill find a way.

 

[jamesjames365]

ok i have 35.544 for the components then...im not sure

 

[shyguy79]

Sorry to jump in Delphi51... this way may be slightly longer but you get an appreciation for what is happening?

I usually convert the polar coordinates (10, 30 deg) into cartesian coordinates (x, y) by using a little trig (SOH CAH TOA)? You can then add these to get the resultant?

For example Sin θ = Opposite / Hypotenuese ... Cos θ = Adjacent / Hypotenuse ... is this ringing any bells yet?

 

[Delphi51]

It doesn't make sense to get "35.544 for the components".
You need TWO components for the first vector and TWO components for the second.
Then you add the x components and add the y components to get TWO totals for x and y. Show us all your work; we'll get you sorted out. Shyguy is saying the same thing I am, with more detail in case you don't understand why the x component of the first vector is 10*cos(30). If you are having difficulty with that, you will need to sketch that vector (draw accurately with a protractor if you can). Then draw sides to make it the hypotenuse of a right triangle. Measure the x and y sides if you can. Calculate them with sine and cosine.

 

[shyguy79]

Something like this...

 

[Delphi51]

That diagram doesn't show the x and y components. I think you would only use that diagram if you were going to do it with Law of Sines and Law of Cosines.

 

[shyguy79]

Sorry, forgot to say - it's just meant to show the sketching of the resultant if done with a rule and protractor...

 

[jamesjames365]

guys i have to say thank you for all the input but i really am starting maths again from scratch so I am reading up on the theorem a little before i jump in and try the equation...

 

[HallsofIvy]

You can use shyguy79's picture to solve the problem without components. You can see that the lower triangle (having the resultant vector as its top line) has two sides of length 10 and 25 and the angle between them is 180- (45+ 30)= 180- 75= 105 degrees. Use the cosine law: c^2= 10^2+ 25^2- 2(10)(25)cos(105).

Once you know that length, you can use the sine law to find the angles.

 

[shyguy79]

You can use shyguy79's picture to solve the problem without components. You can see that the lower triangle (having the resultant vector as its top line) has two sides of length 10 and 25 and the angle between them is 180- (45+ 30)= 180- 75= 105 degrees. Use the cosine law: c^2= 10^2+ 25^2- 2(10)(25)cos(105).

Once you know that length, you can use the sine law to find the angles.

What HallsofIvy said

 

[naviatwal]

My answer came out as
34.75 units at an angle of 40.69 degrees.
Is it correct? Please confirm