Mille89
- 5
- 0
Homework Statement
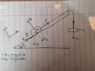
Hi! I am working on a lab-report where we have measured the time a body use up a inclined plane.
i am going to find a expression for the coefficient of friction expressed by the time and acceleration that i have found.
This expression do i need for the next task where i am going to find the kinetic friction.
But i have no idea how i can find the expression
Homework Equations

The Attempt at a Solution