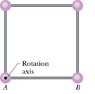
Determining angular speed with only rotational inertia is not feasible, as rotational inertia is a static property that does not provide information about angular speed without additional data. The discussion centers on a specific problem involving four particles forming a square, rotating about an axis when released from rest. Mechanical energy conservation principles are applied to find the relationship between potential and kinetic energy during the rotation. The participants clarify how to calculate rotational inertia and the change in potential energy, leading to a calculated angular speed of approximately 6.28. The conversation emphasizes the importance of understanding mechanical energy conservation in rotational motion.