How to Determine Reactions at Points in Beam Analysis?

[zzinfinity]

Homework Statement

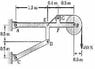
Neglecting the size of the pulley at G, draw the shear and bending moment diagrams for beam AB.

Homework Equations

Fxnet=0
Fynet=0
Netmoment=0

The Attempt at a Solution

\

What I want to do first is figure out the reactions at A and C, however I'm not sure how to do that since there seem to be four unknowns and only three equations. Is this the correct first step, or should I try it another way? Thanks!

 

[nvn]

zzinfinity: Yes, that is the correct first step. No, there are three equations and three unknowns. Hint 1: Is member CD a so-called truss (axial force) member? Give it a try.

 

[zzinfinity]

So does that mean the reaction at c is in the direction of cd? I thought pin connections always had a reaction with unknown direction. Is this not always the case?

 

[SteamKing]

Since member CD is apparently pinned at both ends, the reaction at C will be in line with the line segment CD.

 

[nvn]

So does that mean the reaction at c is in the direction of cd?

Yes.

I thought pin connections always had a reaction with unknown direction. Is this not always the case?

zzinfinity: You are correct. Pin connections generally have a reaction force with (initially) unknown direction. However, this is not the case if a member is (1) pinned at both ends, and (2) has no internal transverse applied load. (Notice, there is no load applied to member CD between points C and D. It thus meets both conditions 1 and 2, making it a truss member.)

Meeting condition 1, alone, does not define a truss (axial force) member.