DrummingAtom
- 657
- 2
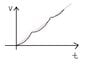
I was driving the other day and thought how I could find the function of my velocity. This would be a rough sketch of data from the velocity of the car. What method could I use to create a function from that graph?
I could assume that the concave parts are x2 then separate them from the flatter parts. That would give me a piecewise function but is there a way to combine all the functions into one?
I drew the red line (y = x) in because that seems like a close approximation. I have learned power and Taylor series but anytime I used those I already knew the function and then came up with the series by taking derivatives. I guess this is more of the numbers only flavor. Any help would be appreciated, thanks.
I could assume that the concave parts are x2 then separate them from the flatter parts. That would give me a piecewise function but is there a way to combine all the functions into one?
I drew the red line (y = x) in because that seems like a close approximation. I have learned power and Taylor series but anytime I used those I already knew the function and then came up with the series by taking derivatives. I guess this is more of the numbers only flavor. Any help would be appreciated, thanks.