How to Find Linear Acceleration Without Cylinder Radius?

[ricles]

Homework Statement

A solid cylinder A of uniform mass given $m_1$ can rotate freely along an axis fixed to a support B of given mass $m_2$, also given. A constant force $F$ is applied at the extremity (point $k$) of a light thread firmly rolled in the cylinder. The friction between the support and the horizontal place is negligible. Find the acceleration at point $k$.

Relevant Equations

Equations of linear and rotational motion.

This comes from a list of exercises, and setting $m_1 = 5.4kg$, $m_2 = 9.3kg$ and $F=5N$, the answer should yield $2.19m/s^2$ (of course, supposing the answer is right).

If I knew the radius $R$ of the cylinder, I could find its momentum and use it to find the linear acceleration. I'm really mystified on how to go about this problem without the radius

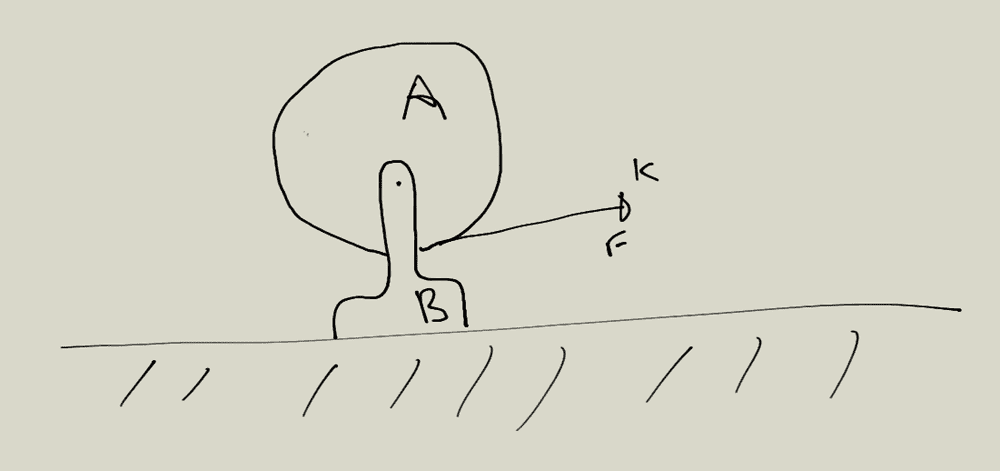
(sorry for the poor drawing :p)

 

[TSny]

If I knew the radius $R$ of the cylinder, I could find its momentum and use it to find the linear acceleration.

It's not clear how you would get from momentum to acceleration.

I'm really mystified on how to go about this problem without the radius

It could be that $R$ cancels out in the calculations so that the answer doesn't depend on $R$.

You will probably need to think about the relation between the linear acceleration of $k$ and the linear acceleration of the center of the cylinder.

 

[ricles]

Yes, that's right. It's actually not complicated after thinking a little, we have ($a_k$ denoting the acceleration at the point k):
$$
\begin{align}
a_{cm} & = \frac{f}{m_1 + m_2} \\
\tau &= f\cdot R = I\cdot \alpha = \left(\frac12 m_1 R^2 \right) \alpha \therefore \alpha = \frac{2f}{m_1R} \\
a_R &= R\cdot \alpha = \frac{2f}{m_1} \text{ (and this is where the R cancels)}\\
a_k &= a_{cm} + a_R = \frac{2f}{m_1} + \frac{f}{m_1 + m_2}
\end{align}
$$
and plugging the values yields the expected result. It was a simple problem - it's just I was "blocked" from seeing it, so to speak. Anyway, thanks for the encouragement