How to know direction of point

[Zirok]

hI,

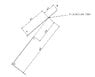
Refering to the attachment, we have set of points A,B,C,D which intersects at a point (Refer Figure)

I have written a forumla in excel to calculate distance d1,d2,d3,d4 from this intersection point.

How would i know that d2 distance is negative ( or in a reverse position) without actually comparing the X,Y positions with respect to Intersection Point.

Is there any other way to do it. ?

Thanks
Zirok

 

[Mark44]

Your attachment is pending approval, so I don't know the details of your problem.

You should not get a negative distance, so if you are, you are doing something wrong. Assuming that your points are in the plane, the distance from a point A(a, a₂) to point B(b₁, b₂) is
\sqrt{(b_1 - a_1)^2 + (b_2 - a_2)^2}.