How to know the cross section in this Figure

[Safinaz]

Hi all,

Do anyone familiar with these analysis of cross section ?

I wonder how to find the cross section of ( p p $\to \gamma \gamma$ b b~) (blue region) in the opposite plot, the y-axis is the number of events divided by 100 GeV with luminosity = 100 $\mbox{fb}^{−1 }$..

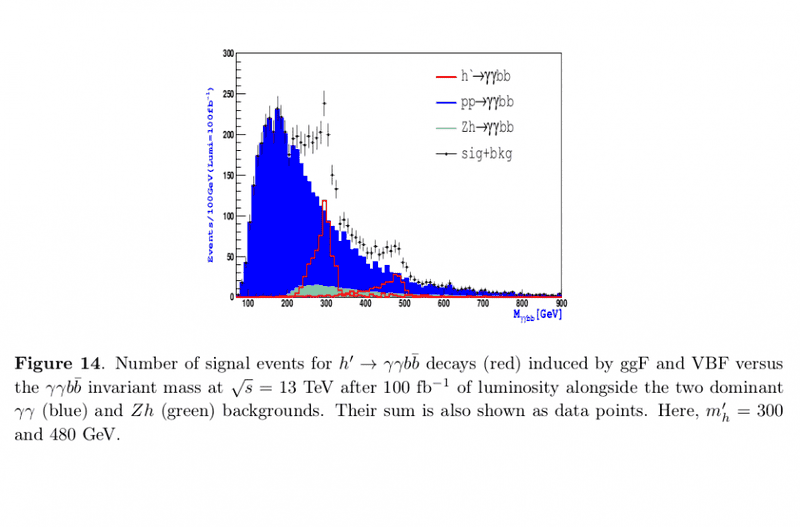The Fig. from [arXiv:1601.07934 [hep-ph]]. It's known that $\sigma \times$ luminosity = Number of events, and also $\mbox{GeV}^{−2}=0.3894~ \mbox{mb}=0.0389~ \mbox{fm}^2$, but i still stuck to find sigma at 250 for instance ..

 

[mfb]

That's a weird axis, but it works. You have to sum over all bins. Let's take the one that goes from 250 to 260 (?), its value is about "110/(100 GeV)" (130 is the sum of pp and Zh, Zh is about 20). The bin width is 10 GeV, so we have 110/(100 GeV) * 10 GeV = 11 events. We have those with 100/fb, so the cross section from this bin is 11/(100/fb) = 0.11 fb. Sum over all bins to get the total cross section.

 

[Safinaz]

I think we can determine the cross section by the maximum of the histogram at around 240 on the y-axis .. so that the number of events =(240/100 )*10=24, the cross section = 24/100 fb =0.24 fb , so we can say p p > 2 gamma 2b as this plot = 0.24 fb, is it right ?

Because actually I don't know how to sum over all bins to get the exact cross section ..

However when I calculate sigma p p > 2 gamma 2 b in standrad model via any cross section calculator like Madgraph , it gives sigma = 346 fb , some thing getting strange here ..

 

[mfb]

I think we can determine the cross section by the maximum of the histogram at around 240 on the y-axis

No we cannot.

Because actually I don't know how to sum over all bins to get the exact cross section ..

Do the calculation I showed for each bin, then add the values.

 

[Safinaz]

Thanx :)

 

[ChrisVer]

I think we can determine the cross section by the maximum of the histogram at around 240 on the y-axis

if instead of taking all the events you want to take only the events that are in a single bin i, what you are calculating is the cross section in that bin (differential cross section d \sigma / dX, where X represents the variable in which you bin the histogram). Obviously you have to integrate that over all X values (sum over all bins) to get the cross section.
Now I wouldn't try to count it with the eye ...