mmmboh
- 401
- 0
Hi, I was asked to prove this identity, I found the determinants for both the left and the right side, and now I basically have to prove that (d/dy)(f(dg/dz))=(df/dy)(dg/dz), the d's are actual partials though. Can anyone give me an idea on how to prove this?
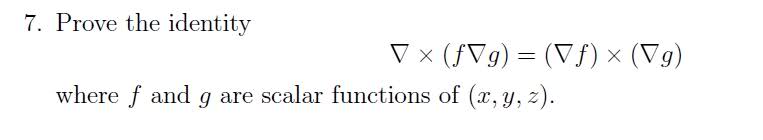
Thanks.
Thanks.