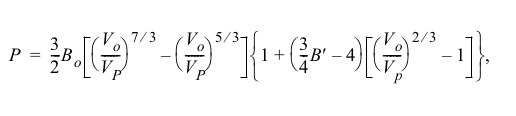Discussion Overview
The discussion centers on the mathematical derivation of the Birch-Murnaghan equation, which describes the volume behavior of materials under high pressure, specifically above 1 GPa. Participants seek clarity on the derivation process and relevant literature.
Discussion Character
- Exploratory, Technical explanation, Debate/contested
Main Points Raised
- One participant inquires about the mathematical derivation of the Birch-Murnaghan equation, emphasizing its application at high pressures.
- Another participant suggests that Birch's original paper may contain a derivation and provides a reference to it, noting that the derivation is isothermal.
- Participants share a link to a PDF that purportedly contains relevant derivation information.
- There is a clarification regarding the notation used in the equation, with one participant suggesting that F refers to Helmholtz free energy rather than force.
Areas of Agreement / Disagreement
There is no consensus on the derivation process itself, and multiple views regarding the sources of information and interpretations of notation are present.
Contextual Notes
The discussion does not resolve the specific steps of the derivation, and participants express uncertainty about the definitions and interpretations of terms used in the equation.