erlend
- 4
- 0
Hello, i have a problem that look's easy to solve but really is not.
It involves a rotating paddle wheel submerged in water and i want to know the force exerted on the wheels and the torque required to rotate it. I have made a simple drawing to illustrate the problem below. I want to use the Drag equation to solve it, even though it is for linear motion, we can convert rotational motion to linear. But since the diameter changes the speed at any radial location and the force is based on a square function i can't get an exact solution for the problem.
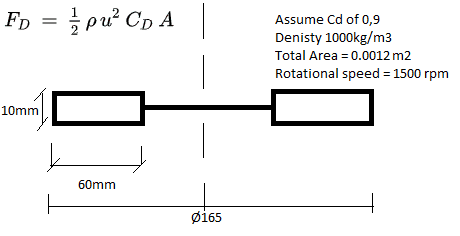
Can you help me with this problem?
It involves a rotating paddle wheel submerged in water and i want to know the force exerted on the wheels and the torque required to rotate it. I have made a simple drawing to illustrate the problem below. I want to use the Drag equation to solve it, even though it is for linear motion, we can convert rotational motion to linear. But since the diameter changes the speed at any radial location and the force is based on a square function i can't get an exact solution for the problem.
Can you help me with this problem?
