Hydrogen, Couloumbs and Quantum Mechanics

[TFM]

Homework Statement

In the derivation of the energy levels in the hydrogen atom one commonly assumes that the nucleus is a point charge. However, in reality the size of the nucleus is of the order of 1fm=10^−15m. Since this is very much smaller than the typical distance of the electron from the nucleus, which is of the order of a_0 \approx 0.5 Angstoms = 0.5 *10^{-10}m, the finite size of the nucleus can be taken into account perturbatively.

a)

Assume that the nucleus of the hydrogen atom is a uniformly charged spherical shell of radius \delta. According to Gauss’ law \int E \cdot dA = Q_{enclosed}/\epsilon_0, the electric field outside this shell is the same as for a point charge at the centre. However, from Gauss’ law also follows that the electric field
inside the shell is zero. Since the force -eE_r on the electron is given by the gradient -\partial V/\partial r of the potential, the potential must thus be constant inside the shell and indistinguishable from the Coulomb potential outside it.

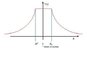
Sketch the potential V (r), find the expression for it, and then find the perturbation \DeltaV relative to the Coulomb potential generated by a point-like nucleus.

b)

Use the ground-state wave function for a hydrogen atom with a point-like nucleus,

\Phi_{100}(r,\theta, \phi) = \frac{1}{\sqrt{\pi a_0^3}}e^{-r/a_0}

and calculate the shift of the ground-state energy due to the distribution of the nuclear charge overa finite spherical shell to first order in the perturbation.

c)
Expand the result of (b) in powers of \delta/a_0, retain only the first non-vanishing term, and thus show that the ground-state energy shift is approximately

\Delta E_1 \approx \frac{e^2}{6\pi\epsilon_0}\frac{\delta^2}{a_0^3}

Homework Equations

Given on sheet:

e^x = \Sigma \frac{x^n}{n!}

The Attempt at a Solution

Okay B, I think is a normal inverse square law graph, similar to that of gravity. It goes up with constant gradient until it reaches the radius R, then decreases inverse square law curve.

I am not sure however what to do for b). Do I need to insert the potential into a Schrödinger Equation?

 

[TFM]

Okay, I have worked out that for b), I need to use the equation:

\Delta E = \int^{\infty}_{-\infty}\phi^*_n \Delta V(r) \phi_n

Now they give you phi, but I am slightly unsure as to how I get the Delta V(r). I thunk this bit is also part of a).

Any helpful suggestions of how to get this value?

Also, I think I have the graph wrong. I t should be more of a plateau, with the sides curving downwards, as attached.