mateomy
- 305
- 0
This is technically a physics problem but its straight outta my calculus book...
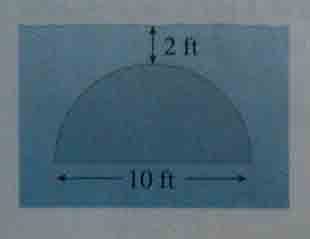
The instructions are to express the force as an integral and evaluate it.
My problem is just the initial set up. I've tried a couple of different ways and none of them get me the answer that I am seeing in the back of the book.
I know that I am looking at a half circle so that would be \frac{1}{2}\pi(r^2) and I would be evaluating it with respect to x (or y, depending on my axes). Also, the semicircle is submerged 2ft below the surface, so is that (total depth - y), (7 - y)? I am super confused.
On top of all this, I don't even know what upper and lower bounds I should be evaluating it at. 2 to 7? 0 to 5?
All in all this is the closest -yet, incorrect- way I've come to setting it up. Oh, I am using \delta as my weight density (62.5 lb/ft^3).
<br /> \int\limits_?^? \delta \frac{\pi}{2} (\sqrt{r^2 - y^2})^2 (7 - y) dy<br />
Completely lost, any help or nudges in the right direction would be tremendously appreciated.
The instructions are to express the force as an integral and evaluate it.
My problem is just the initial set up. I've tried a couple of different ways and none of them get me the answer that I am seeing in the back of the book.
I know that I am looking at a half circle so that would be \frac{1}{2}\pi(r^2) and I would be evaluating it with respect to x (or y, depending on my axes). Also, the semicircle is submerged 2ft below the surface, so is that (total depth - y), (7 - y)? I am super confused.
On top of all this, I don't even know what upper and lower bounds I should be evaluating it at. 2 to 7? 0 to 5?
All in all this is the closest -yet, incorrect- way I've come to setting it up. Oh, I am using \delta as my weight density (62.5 lb/ft^3).
<br /> \int\limits_?^? \delta \frac{\pi}{2} (\sqrt{r^2 - y^2})^2 (7 - y) dy<br />
Completely lost, any help or nudges in the right direction would be tremendously appreciated.