Hydrostatic forces on a hinged gate

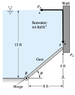
[member 428835]

I'm trying to just find the hydrostatic force on the hinge of the gate in the image attached, and while not labeled, the thickness out of the page is $w=5$. My thoughts are to set up this integral $$\vec{F}_p = \iint \rho g y \hat{n}\, dA = w \rho g \int_0^8 y \left( \frac{-dx\hat{i}+dy\hat{j}}{\sqrt{dx^2+dy^2}} \right)\, \sqrt{dx^2+dy^2}\\
= w \rho g \int_0^8 y \left(-dx\hat{i}+dy\hat{j} \right)\\
= w \rho g \int_0^8 y \left(y'(x)\hat{j}-1\hat{i} \right) \, dx\\
=5\cdot 64 \int_0^8 \left(9 + \frac{3 x}{4}\right)(\frac{3}{4}\hat{j}-\hat{i})\, dx\\
=-30720 \hat{i} + 23040 \hat{j}$$
where the magnitude of the last expression gives me the correct answer of the magnitude of $\vec{F}_p=38,400$ lbf. So when finding the force on the hinge I would say it is simply $-30720 \hat{i} + 23040 \hat{j}$ but the book says something else. Where am I going wrong?

 

[billy_joule]

Where am I going wrong?

Some of the force on the gate is supported by the non hinged end (at A). Taking moments about point A is probably the quickest way to find the force on the hinge.

 

[member 428835]

Thanks, your response makes perfect sense! Could you help me set up this integral if the water was instead below the gate?

 

[Nidum]

Problem in #1 can be solved in a few lines using basic trig and simple arithmetic ?

 

[Chestermiller]

Josh,

What Nidum is referring to is this: Draw a dashed horizontal line from point A to the left, and draw a dashed vertical line from point B vertically upward. Then consider the fluid contained in the region between the gate and the dashed lines. Do a force balance on this fluid in the horizontal and vertical directions. This will quickly give you the horizontal and vertical components of the force exerted by the gate on the fluid (and, by Newton's 3rd law, the fluid on the gate).