mbrmbrg
- 485
- 2
hydrostatic pressure (basic, basic stuff)
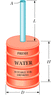
In Figure 14-31 (attatched), an open tube of length L = 1.8 m and cross-sectional area A = 4.6 cm2 is fixed to the top of a cylindrical barrel of diameter D = 1.2 m and height H = 1.8 m. The barrel and tube are filled with water (to the top of the tube).
(a)Calculate the ratio of the hydrostatic force on the bottom of the barrel to the gravitational force on the water contained in the barrel.
(b)Why is that ratio not equal to 1.0? (You need not consider the atmospheric pressure.)
P=F/A
P=P_0+\rho gh
mg=\rho Vg
If it please the honored members of the site, their humble servant shall not blabber on with the method to the solution. For part (a) I got 2, which is the correct answer.
But part (b) has me stumped--my current answer reads "why would the ratio be 1?" I think I might be able to give a slightly more mature answer if I knew what logical fallacy I am supposed to be disproving...
Homework Statement
In Figure 14-31 (attatched), an open tube of length L = 1.8 m and cross-sectional area A = 4.6 cm2 is fixed to the top of a cylindrical barrel of diameter D = 1.2 m and height H = 1.8 m. The barrel and tube are filled with water (to the top of the tube).
(a)Calculate the ratio of the hydrostatic force on the bottom of the barrel to the gravitational force on the water contained in the barrel.
(b)Why is that ratio not equal to 1.0? (You need not consider the atmospheric pressure.)
Homework Equations
P=F/A
P=P_0+\rho gh
mg=\rho Vg
The Attempt at a Solution
If it please the honored members of the site, their humble servant shall not blabber on with the method to the solution. For part (a) I got 2, which is the correct answer.
But part (b) has me stumped--my current answer reads "why would the ratio be 1?" I think I might be able to give a slightly more mature answer if I knew what logical fallacy I am supposed to be disproving...
Attachments
Last edited: