You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
I am having a hard time defining theta in Torque=rFsin(theta)
AI Thread Summary
Theta in the torque equation Torque = rFsin(theta) represents the angle between the position vector (r) and the force vector (F). In the context of a pulley, the tension forces are tangential to the pulley, meaning they act along the circular path of the pulley. When a force is applied at the point of application, it is at a 90-degree angle to the radius drawn from the center of the pulley to that point. Therefore, for a pulley, theta is typically 90 degrees. Understanding this relationship clarifies the calculation of torque in rotational systems.
Physics news on Phys.org
Doc Al
Mentor
- 45,578
- 2,435
In general, θ would be the angle between the position vector (r), which describes the point of application with respect to some axis, and the force vector (F).dadiezel07 said:Can someone dummify what theta represents in Torque = rFsin(theta)?
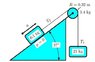
No. Assuming you are trying to express the torque on the pulley, realize that the tensions are tangential to the pulley.if my understanding of theta is correct for this problem theta would be 53 degrees.
dadiezel07
- 3
- 0
Doc Al said:No. Assuming you are trying to express the torque on the pulley, realize that the tensions are tangential to the pulley.
When you say they are tangential to the pulley, can you explain a little furthur.
Thats another subject I can't quite wrap my head around is the definition on tangential, is it the word to describe "linear" equations?
I have been continuing the subject without complete understanding of everything this is my attempt at understanding everything because my book does a horrible job.
Doc Al
Mentor
- 45,578
- 2,435
I mean that the line of action of the tension force (which is the line that the ropes make) is tangential to the circle that is the pulley. Which means that if you draw a radius to the point of application of the force, the force would be at 90° to the radius.dadiezel07 said:When you say they are tangential to the pulley, can you explain a little furthur.
dadiezel07
- 3
- 0
so in the case of the pulley will the theta angle always be 90 degrees?
Doc Al
Mentor
- 45,578
- 2,435
Yes.dadiezel07 said:so in the case of the pulley will the theta angle always be 90 degrees?
TL;DR Summary: I came across this question from a Sri Lankan A-level textbook.
Question - An ice cube with a length of 10 cm is immersed in water at 0 °C. An observer observes the ice cube from the water, and it seems to be 7.75 cm long. If the refractive index of water is 4/3, find the height of the ice cube immersed in the water.
I could not understand how the apparent height of the ice cube in the water depends on the height of the ice cube immersed in the water. Does anyone have an...
Kindly see the attached pdf. My attempt to solve it, is in it.
I'm wondering if my solution is right. My idea is this: At any point of time, the ball may be assumed to be at an incline which is at an angle of θ(kindly see both the pics in the pdf file). The value of θ will continuously change and so will the value of friction.
I'm not able to figure out, why my solution is wrong, if it is wrong .
Similar threads
- Replies
- 11
- Views
- 1K
- Replies
- 1
- Views
- 1K
- Replies
- 4
- Views
- 864
- Replies
- 24
- Views
- 2K
- Replies
- 6
- Views
- 917
- Replies
- 8
- Views
- 271
- Replies
- 5
- Views
- 1K
- Replies
- 5
- Views
- 703
- Replies
- 5
- Views
- 901
- Replies
- 5
- Views
- 2K
Hot Threads
-
Torque biomechanics
- Started by Naucus
- Replies: 6
- Introductory Physics Homework Help
-
Work Done in slowly pulling a thread
- Started by Bling Fizikst
- Replies: 28
- Introductory Physics Homework Help
-
How do you calculate the pull of this piston?
- Started by vdance
- Replies: 27
- Introductory Physics Homework Help
Recent Insights
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 26
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 3
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math