Identifying the Potential and Eigenfunction for Lowest Energy

[justanovice]

Homework Statement

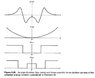
Consider the eigenfunction in the top part of the figure.
(a) Which of the three potentials illustrated in the bottom part of the
figure could lead to such an eigenfunction? Give qualitative
arguments to justify your answer. (b) The eigenfunction shown
is not the one corresponding to the lowest allowed energy for the
potential. Sketch the form of the eigenfunction which does
correspond to the lowest allowed energy E1. (c) Indicate on
another sketch the range of energies where you would expect
discretely separated allowed energy states, and the range of
energies where you would expect the allowed energies to be
continuously distributed. (d) Sketch the form of the eigenfunction which corresponds to
the second allowed energy E2. (e) To which energy level does the eigenfunction presented
on top of the figure correspond

I've attached the figure, but It might be easier to read in this file i found on the internet (problem #5): http://www.phys.ncku.edu.tw/~ccheng/MP2011/HW2_SE.pdf

The Attempt at a Solution

I have already done part (a) by identifying the sign of ψ and (V-E). I concluded that the correct potential is the last one on the bottom. You can see my solution in the attachment.
For part (b), i think the sketch should have two peaks, one in each classically allowed region (B/C and E/F in my drawing) since this is the minimum amount of oscillations that will work.
However, this makes me think the answer to part (e) is energy level two.
Which makes part (d) confusing.
Also, I'm not sure what part (c) means by "discretely separated allowed allowed energy states" and continuously distributed allowed energies.

Any help would be greatly appreciated.

 

[diazona]

Hm... I follow your reasoning about the wavefunction shown being the second energy level. I'm not sure what they're getting at there but I'll see if someone else can figure it out.

As for part (c), the problem is talking about bound states and scattering states. Or alternatively, think of it like this: can you identify certain significant energies at which the behavior of the corresponding eigenfunction changes? In other words, for some particular energy E_A there is a qualitative difference between a wavefunction corresponding to E < E_A and a wavefunction corresponding to E > E_A. What energy is that? What is another energy E_B at which the same could be said?

 

[justanovice]

thank you!, i understand part (c) now.

my final is tomorrow and i was told there would be a problem similar to this, so any insight on parts (d) and (e) would help.

 

[vela]

There are two possible wave functions that have one peak in the B/C and E/F. One is odd, and one is even.

 

[Duave]

I think I have the same exact final as justanovice...exactly the same class...lol!