GRice40
- 20
- 0
Homework Statement
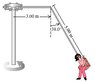
The "Giant Swing" at a county fair consists of a vertical central shaft with a number of horizontal arms attached at its upper end. Each arm supports a seat suspended from a 5.00m long cable, the upper end of which is fastened to the arm at a point 3.00 m from the central shaft. Find the time of one rotation if the angle produced from the cable connecting to the arm is 30 degrees from vertical.
Homework Equations
Circumference= distance = 2 (pi) R
Acceleration = V^2/R
F = m(V^2/R)
The Attempt at a Solution
I honestly have no clue how to do this one. I keep working myself in circles, which doesn't seem to be getting anything accomplished. Any help on where I should start?