AbigailM
- 46
- 0
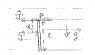
For prelim preparation. I've also included a figure of the problem.
A stick of length l is suspended by one end at point P so that it hangs vertically and so that the top end of the stick does not move. A horizontal impulse J is applied perpendicular to the stick a distance a below the point of suspension. In general there will be an opposite impulse J' that must be given at the top of the stick (point P) to keep its point of suspension fixed. Find the distance a such that J'=0.
\tau=r\hspace{1 mm} x\hspace{1 mm} F
\tau=I\alpha
L=T-U
L=\frac{1}{2}I\dot{\theta}^{2} +mg\frac{l}{2}cos\theta
Using Lagrange's Equations
I\alpha=-mg\frac{l}{2}sin\theta
Equating the two equations for torque and setting r=a
I\alpha = aFsin\theta
Equate the last to equations
aFsin\theta=-mg\frac{l}{2}sin\theta
Solving for F
F=-\frac{mgl}{2a}
Therefore J is
J=-\frac{mglt}{2a}
So J' is
J'=\frac{mglt}{2a}
Is this looking correct? Gracias!
Homework Statement
A stick of length l is suspended by one end at point P so that it hangs vertically and so that the top end of the stick does not move. A horizontal impulse J is applied perpendicular to the stick a distance a below the point of suspension. In general there will be an opposite impulse J' that must be given at the top of the stick (point P) to keep its point of suspension fixed. Find the distance a such that J'=0.
Homework Equations
\tau=r\hspace{1 mm} x\hspace{1 mm} F
\tau=I\alpha
L=T-U
The Attempt at a Solution
L=\frac{1}{2}I\dot{\theta}^{2} +mg\frac{l}{2}cos\theta
Using Lagrange's Equations
I\alpha=-mg\frac{l}{2}sin\theta
Equating the two equations for torque and setting r=a
I\alpha = aFsin\theta
Equate the last to equations
aFsin\theta=-mg\frac{l}{2}sin\theta
Solving for F
F=-\frac{mgl}{2a}
Therefore J is
J=-\frac{mglt}{2a}
So J' is
J'=\frac{mglt}{2a}
Is this looking correct? Gracias!
Attachments
Last edited: