1337pHysiX
- 2
- 0
ok I'm desperate now lol n this is my first time on PF.
I've just had an exam and I'm sure i got this question wrong. But i'd like to know:
the normal reaction force and the tension/Force F.
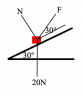
The question is: There is this object that has a weight of 20N. It is on an inclined plane that is 30 degrees and it is held by a force 30 degrees to the plane. Determine the normal reaction force and the tension in the string.
Please give me as much relevant working as possible. Thank you for your help!
I have attached the diagram/question.
I've just had an exam and I'm sure i got this question wrong. But i'd like to know:
the normal reaction force and the tension/Force F.
The question is: There is this object that has a weight of 20N. It is on an inclined plane that is 30 degrees and it is held by a force 30 degrees to the plane. Determine the normal reaction force and the tension in the string.
Please give me as much relevant working as possible. Thank you for your help!
I have attached the diagram/question.
Attachments
Last edited: