Homework Help Overview
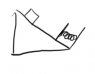
The problem involves a mass on a frictionless inclined plane with a spring underneath. The mass is given as 2.5 kg, the incline angle is 40°, and the height is 1.6 m. The spring has an initial extension of 30 cm and is compressed by a maximum of 12 cm. The goal is to determine the spring constant "k".
Discussion Character
- Exploratory, Assumption checking, Problem interpretation
Approaches and Questions Raised
- Participants discuss the conservation of energy principle, questioning how to apply it given the inclined plane's geometry. There is uncertainty about the correct value for "x" in the energy equations, with some suggesting it should be the compression of the spring while others consider the initial and final lengths of the spring.
Discussion Status
Participants are exploring different interpretations of the problem, particularly regarding the height measurement and the relationship between gravitational potential energy and the spring's compression. Some guidance has been offered about the height difference and the need to consider the geometry of the situation.
Contextual Notes
There is a discussion about the orientation of the spring and whether the height should be measured relative to the incline or from the ground. Participants are also clarifying the definitions of potential energy in this context.