Inclined throw in a vertical loop

[Karol]

Homework Statement

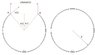
A small ball rotates in a vertical loop of radius R. it's velocity is the minimal required to stay in the loop.
Now the loop is cut at an angle $\alpha$ and the ball shoots out of it.
Express $\alpha$ so that the ball falls back into the loop and continues turning.

Homework Equations

The horizontal distance in an inclined throw: $x=\frac{V^2\sin(2\theta)}{g}$
The acceleration in circular movement: $a=\frac{V^2}{R}$

The Attempt at a Solution

The velocity at the highest point, so it won't fall: $V=\sqrt{gR}$
The difference between the highest point and the cut in the loop, point A: $h=R\left(1-\cos\frac{\alpha}{2}\right)$
Energies between the highest point and A:
$$\frac{mgR}{2}=-mgR\left(1-\cos\frac{\alpha}{2}\right)+\frac{mV^2}{2}$$
$$\rightarrow V^2=gR\left(3-2\cos\frac{\alpha}{2}\right)$$
Our horizontal distance:
$$x=2R\sin\left(\frac{\alpha}{2}\right)$$
The throw angle $\theta$ is $\frac{\alpha}{2}$
The horizontal distance at inclined throw with our velocity and angle:
$$x=\frac{gR\left(3-2\cos\frac{\alpha}{2}\right)\sin \alpha}{g}=R\left(3-2\cos\frac{\alpha}{2}\right)\sin \alpha$$
This distance equals the distance between points A and B:
$$R\left(3-2\cos\frac{\alpha}{2}\right)\sin \alpha=2R\sin\left(\frac{\alpha}{2}\right)$$
$$4\cos^2\frac{\alpha}{2}-6cos\frac{\alpha}{2}+1=0$$
And it's wrong, it should be $\alpha=120^0$

 

[Karol]

I made a mistake. the last formula should be:
$$2\cos^2\frac{\alpha}{2}-3\cos\frac{\alpha}{2}+1=0$$
$$\alpha=90^0$$
And it should be 120

 

[ehild]

There are two roots for cos(a/2). One is 1, but that corresponds to a vertical throw. The other is cos(a/2)=1/2, that is alpha/2 = 60°, alpha= 120°.

ehild

 

[Karol]

Thanks very much, a silly mistake