Induced emf in a square loop at rest

PERE'S LAW:In summary, the task is to determine the emf induced in a square loop, with sides of 12.0 cm and 15.0 cm, if the loop is at rest and the current in a straight wire is given by I(t) = (15.0 A)sin(2500t) where t is in seconds. The equation for the emf is given by emf=(uIv(a^2))/(2pi(a+b)b), which is derived from Faraday's law.
  • #1
iknowles
1
0

Homework Statement



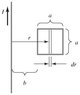
Determine the emf induced in the square loop in the figure if the loop stays at rest and the current in the straight wire is given by I(t) = (15.0 A)sin(2500t) where t is in seconds. The distance a is 12.0 cm, and b is 15.0 cm.

Homework Equations



In the question prior to this one in the homework, emf=(uIv(a^2))/(2pi(a+b)b)



The Attempt at a Solution



I initially attempted to just substitute the equation for I into the emf equation but that hasn't worked. I'm clueless on how to proceed.

Please help! Thank you!
 

Attachments

  • GIANCOLI.ch29.p26.jpg
    GIANCOLI.ch29.p26.jpg
    4.4 KB · Views: 651
Physics news on Phys.org
  • #2
This is not just an Ampere's law problem. Faraday's law also applies.

AM
 

FAQ: Induced emf in a square loop at rest

What is induced emf in a square loop at rest?

Induced emf in a square loop at rest refers to the phenomenon where an electric potential is created in a stationary square loop by a changing magnetic field. This is known as electromagnetic induction and is described by Faraday's law of induction.

How is induced emf calculated in a square loop at rest?

The induced emf in a square loop at rest can be calculated by multiplying the rate of change of the magnetic flux through the loop by the number of turns in the loop. This can be represented mathematically as E = -N(dΦ/dt), where E is the induced emf, N is the number of turns, and dΦ/dt is the rate of change of magnetic flux.

What factors can affect the induced emf in a square loop at rest?

The induced emf in a square loop at rest can be affected by several factors, including the strength and direction of the magnetic field, the size and shape of the loop, and the speed at which the magnetic field changes. The material of the loop can also have an impact on the induced emf.

How does the direction of the induced emf in a square loop at rest relate to the direction of the changing magnetic field?

According to Lenz's law, the direction of the induced emf in a square loop at rest will be such that it opposes the change in magnetic field that caused it. This means that if the magnetic field is increasing, the induced emf will be in the opposite direction to the change, and if the magnetic field is decreasing, the induced emf will be in the same direction as the change.

What are the applications of induced emf in a square loop at rest?

Induced emf in a square loop at rest has several practical applications, such as in generators and transformers. In generators, the induced emf is used to convert mechanical energy into electrical energy, while in transformers, it is used to change the voltage of an electrical system. Induced emf is also used in devices such as induction cooktops and magnetic levitation systems.

Similar threads

EMF in a square loop due to magnetic field from an infinite wire
Replies
10
Views
9K
What EMF is induced in the loop at t=0?
Replies
6
Views
2K
Need someone to check my equations and work on this induced EMF problem
Replies
1
Views
992
How Accurately Can Induced EMF Represent Batteries in Circuit Problems?
Replies
8
Views
2K
Induced current in two connected loops
Replies
5
Views
2K
The Magnitude of Induced EMF in a Moving Rod?
Replies
8
Views
3K
Zero Induced EMF: Find Rate of B Change for Problem 9
Replies
3
Views
1K
Induced EMF and current in the circuit
Replies
10
Views
2K
What is the amplitude of induced EMF in a magnetic dipole antenna?
Replies
3
Views
2K
Electromotive force (EMF) of a circular loop wire
Replies
3
Views
2K

Hot Threads

Recent Insights

Back
Top