Induced emf in a wire hard mathematically

[fluidistic]

Homework Statement

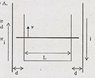
See picture for clarity.
There are 2 infinite wires carrying a current i, one wire does it in the upward direction and the other wire in the downward direction. They are separated by a distance L+2d.
Between them lies a circuit such that the part that moves with a velocity v upward has a resistance R and the rest of the circuit has a negligible resistance.
1)Calculate the induced current through the rod moving at constant velocity v.
2)Calculate the force needed to maintain the constant velocity. (applied by an external agent)
3)The work done by the external agent by unit of time.

Homework Equations

None given.

The Attempt at a Solution

First I calculated the magnetic field between the 2 wires. I used Ampere's law. I reached $$B=\frac{\mu _0 I}{2\pi r}+\frac{\mu _0 I}{2\pi (L+2d-r)}$$, pointing into the sheet.
Now $$V=RI\Rightarrow I=\frac{V}{R}=-\frac{d\Phi _B}{dt}\cdot \frac{1}{R}$$.
So I must find $$\frac{d \Phi _B}{dt}$$.
First, I'm looking for $$\Phi _B$$.
I believe that $$\Phi _B = A\cdot B_{\text{enclosed}}$$.
So I integrated the expression I had found of B from d to L-d, which gave me $$B_{\text{enclosed}}=\frac{\mu _0 I}{2\pi r}\left [ \ln \left ( \frac{L-d}{d} \right) + \ln \left ( \frac{d+L}{3d} \right ) \right ]$$.
Then $$\frac{d \Phi _B}{dt}=LvB_{\text{enclosed}}$$, thus $$I=-\frac{Lv B_{\text{enclosed}}}{R}$$.

It was so messy to calculate, I'm sure at 99.9999999999% I've made at least an error...
Could someone confirm it? Or at least tell me if my reasoning was right.
Thanks in advance.

 

[Redbelly98]

Hi there ,

You're vaguely on the right track, but here are a few comments:

"B_enclosed" does not have any real meaning. Instead, you are actually trying to find

Φ_B = ∫B·dA​

for the loop.

After writing B·dA in terms of r, the distance from a wire, the integration limits will be from d to L+d These are the distances from the vertical parts of the loop to either of the wires.

The final expression for Φ_B should not depend on r (an integration variable), and should depend on time t somehow.

 

[fluidistic]

Thank you so much Redbelly. I'm going to try tomorrow (a bit late for now).
Wow, so when I will calculate $$\frac{d \Phi _B}{dt}$$, it will go even messier since ∫B·dA depends on time!
I'll probably ask for further help tomorrow... but as of now, I say a big thank you.

 

[Redbelly98]

Okay, good luck. By the way, it will be a fairly simple time-dependence, and a simple derivative.

 

[fluidistic]

Okay, good luck. By the way, it will be a fairly simple time-dependence, and a simple derivative.

Here's my attempt: ΦB=∫B·dA=$$B\cdot A$$ because the 2 vectors are orthogonals. This gives me ΦB$$=\frac{\mu _0 I}{2\pi} \left[ \frac{1}{r}+\frac{1}{L+2d-r} \right] Lvt$$.
Integrating, $$\int_d^{L+d} \Phi _B dr=\frac{\mu _0 I Lvt}{2\pi} \left[ \ln \left ( \frac{L+d}{d} \right) +\ln \left ( \frac{L+3d}{d} \right ) \right ]$$.
Derivating with respect to time, $$\frac{d \Phi _B}{dt}=\frac{\mu _0 I Lv}{2\pi} \left[ \ln \left ( \frac{L+d}{d} \right) +\ln \left ( \frac{L+3d}{d} \right ) \right ]$$, thus $$I=-\frac{\mu _0 I Lv}{2\pi} \left[ \ln \left ( \frac{L+d}{d} \right) +\ln \left ( \frac{L+3d}{d} \right ) \right ] \cdot \frac{1}{R}$$. Unfortunately I cancels out... What am I doing wrong?

 

[rl.bhat]

Here's my attempt: ΦB=∫B·dA=$$B\cdot A$$ because the 2 vectors are orthogonals. This gives me ΦB$$=\frac{\mu _0 I}{2\pi} \left[ \frac{1}{r}+\frac{1}{L+2d-r} \right] Lvt$$.

I didn't understand how did you get expression for Φ_B.
Inside the loop field due to two current carrying conductors is identical.
So net Φ_B= 2*Lvt*μ_o/2π*Intg[1/r]*dr between the limits d to (d+L).

 

[Redbelly98]

Use rl.bhat's hint, just do the integral for one wire and multiply the result by 2.

Also, dΦ_B/dt (1/R) gives you the current in the loop, not the current in the outside wires. They are different currents.

 

[fluidistic]

I didn't understand how did you get expression for Φ_B.
Inside the loop field due to two current carrying conductors is identical.
So net Φ_B= 2*Lvt*μ_o/2π*Intg[1/r]*dr between the limits d to (d+L).

Ok I made an error. Without using the trick of multiplying by 2 the integral of the first wire, I do it the hard way.
Here's my new attempt: From Ampere's law, the total electric field is given by $$B(r)=\frac{\mu _0I}{2\pi} \left[ \frac{1}{r}+\frac{1}{r-2d-L} \right]$$.
Do you buy that? If so, then you should also buy that $$B\cdot dA=\frac{\mu _0I}{2\pi} \left[ \frac{1}{r}+\frac{1}{r-2d-L} \right] \codt Lvdt$$.
Integrating from d to L+d, I reached $$\Phi _B= \frac{Lvdt \mu _0 I}{2\pi}\int _d ^{L+d} \frac{1}{r}+\frac{1}{r-2d-L} dr=\frac{Lvdt \mu_0 I}{2\pi} \cdot \left [ \ln \left ( \frac{L+d}{d} \right ) + \ln \left ( \frac{d}{L+d} \right) \right ]$$. It seems to me it's worth 0...
Where did I go wrong?

 

[rl.bhat]

The distance of a point from the second wire in terms of r is (2d + L - r). Now you will get the required result. When you find magnetic field due to current carrying conductor, distance should be always positive. In your expression for second wire it is negative. That is why you got zero result.

 

[fluidistic]

The distance of a point from the second wire in terms of r is (2d + L - r). Now you will get the required result. When you find magnetic field due to current carrying conductor, distance should be always positive. In your expression for second wire it is negative. That is why you got zero result.

Ok thank you very much. So I'm the same case as before. I get $$\Phi _B =\frac{\mu _0 I vLdt}{2\pi} \left [ \ln \left ( \frac{L+d}{d} \right ) + \ln \left ( \frac{L+3d}{d}\right ) \right ]$$.
I don't know what I'm missing... I'm sure it's wrong. Now I have to differentiate with respect to time...

 

[Redbelly98]

The term in question is a result of doing this integral:

$$\int_{d}^{L+d}\frac{1}{L+2d-r}dr =-ln(L+2d-r)|_{d}^{L+d}$$

L+2d-r is the distance to the right-hand wire here.