Induced Emf in an Inductor in an LRC circuit

[asb5468]

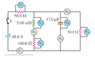
Homework Statement

In the circuit shown in the figure, the switch S is closed at time t=0 with no initial charge on the capacitor. What is the induced emf if the inductor at time t=0?

Homework Equations

ε=-LdI/dt

The Attempt at a Solution

Initially the inductor acts like a broken wire in that no current can go through it so the potential difference across the 100 Ω resistor is 0. The capacitor initially has 0 resistance, so all the current will flow through there and the voltage across the 50Ω resistor in parallel with the capacitor (V4) will also be zero. So a time t=0 it acts like a simple circuit with resistance 50 Ω and εbattery 40 V. I am unsure if there would also be a potential difference across the inductor due to an induced emf. I don't really know how to find the current as a function of time for this combination circuit so I'm not sure if dI/dt would then be zero, making the induced emf zero. Any help is appreciated!

 

[paisiello2]

dI/dt does not equal zero in the inductor. Although at time t=0 there is no current in the inducter, at some future time there will be a current in the inductor.

 

[SammyS]

dI/dt does not equal zero in the inductor. Although at time t=0 there is no current in the inducter, at some future time it won't be.

To expand on this, what is the rate of change of the voltage across the capacitor immediately after the switch is closed?

 

[rude man]

The rate of change of voltage on, and current thru, the capacitor is irrelevant.
What is the initial voltage across the capacitor? Ergo, across the L-R arm? Ergo, across L?

 

[SammyS]

The rate of change of voltage on, and current thru, the capacitor is irrelevant.
What is the initial voltage across the capacitor? Ergo, across the L-R arm? Ergo, across L?

Yes.

rude man is correct.

I must have had some brain flatulence .

 

[rude man]

Yes.

rude man is correct.

I must have had some brain flatulence .

That's funny, Sammy!
Anyway, welcome to the club ...