Hyacinth42
- 9
- 0
Two straight conducting rails form a right angle where their ends are joined. A conducting bar in contact with the rails starts at the vertex at time t = 0 and moves with a constant velocity of 7.00 m/s along them, as shown in Fig 31-44. A magnetic field with B = 0.350 T is directed out of the page.
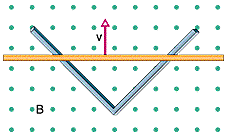
(a) Calculate the flux through the triangle formed by the rails and bar at t = 2.50 s
(b) Calculate the magnitude of the emf around the triangle at that time.
(c) If we write the emf as E = at^{}n, where a and n are constants, what is the value of n?
---------
Alright, I can figure this out, only I don't know how to find the rate of change of the length of the two non-moving bars. With that, I could find the area at t = 2.50 s, and the change of the magnetic flux, and I could muddle through the last one ;)
(a) Calculate the flux through the triangle formed by the rails and bar at t = 2.50 s
(b) Calculate the magnitude of the emf around the triangle at that time.
(c) If we write the emf as E = at^{}n, where a and n are constants, what is the value of n?
---------
Alright, I can figure this out, only I don't know how to find the rate of change of the length of the two non-moving bars. With that, I could find the area at t = 2.50 s, and the change of the magnetic flux, and I could muddle through the last one ;)