Alice-Shallom
- 4
- 0
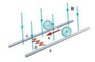
In the figure attached below, the rolling axle, 1.50 m long, is pushed along horizontal rails at a constant speed u = 3.00 m/s. A resistor R= 0.400 Ω is connected to the rails at points a and b, directly opposite each other. (The wheels make good electrical contact with the rails, and so the axle, rails, and R form a closed-loop circuit. The only significant resistance in the circuit is R.) There is a uniform magnetic field B= 0.0800 T vertically downward.
a)Find the induced current I in the resistor.
b)What horizontal force F is required to keep the axle rolling at constant speed?
c)Which end of the resistor, a or b, is at the higher electric potential?
d)After the axle rolls past the resistor, does the current in R reverse direction?
a)Find the induced current I in the resistor.
b)What horizontal force F is required to keep the axle rolling at constant speed?
c)Which end of the resistor, a or b, is at the higher electric potential?
d)After the axle rolls past the resistor, does the current in R reverse direction?