Inelastic collision Two angles and final velocities

[-PhysicsMajor-]

Homework Statement

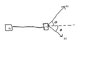
Consider an inelastic collision between two blocks on a horizontal plane. Block M1 is moving with velocity V_o and collides with block M2 which is at rest. During the collision a fraction Q of the original kinetic energy is lost. It is observed that M1 is deflected by an angle theta (above the x axis), and M2 is deflected at an angle phi (below the x axis). After the collision M1 is moving to the right.

Find the angle phi, and the final velocities of the blocks.

M1=2kg
M2=4kg
V_o=10m/sec
Theta=30^o
Q=.2

Homework Equations

Inital Momentum = Final Momentum (M1_iV_o+M2_iV_o =M1_fV_f+M2_fV_f)

KE_f = (1-Q)KE_i

*I'm sure there are more but this is what I have from class.

The Attempt at a Solution

Finding the final KE was easy enough using the above equation: KE inital =100 KE final =80

Then I tried to split them up in the x and y components. They both start with zero in the y direction and only M1 has initial momentum in the x direction. In the Y direction after the impact I got some sin and cos directions
So M1_iV_o = M1V1_fCos(theta)+M2V2_fcos(phi)+M1V1_f-M2V2_fsin(phi) (negative because it is below the x axis)
If that is right (big if) I have no clue where to go from here. I really don't know how to turn the final kinetic energy into two different objects and I REALLY don't know how to find that phi angle. I'm at a complete loss.

This is my first post here so hopefully formatted the question correctly. This stuff is really stressing me out. Every time I think that I've stumbled upon something useful online, it just seems way to simple, which is pretty much a guarantee that it can't help me. Our homework consists of just a few problems over the course of a week, and when he shows examples in class my professor fills several chalkboards full of calculations. So anything that is a quick answer must be wrong.

I don't want the answer, I just need a nudge in the right direction of how to even set up the problem. I have not found a single thing online that can help with these intermediate inelastic collisions with two objects of a different mass.

This forum is my last hope.

*Way too many words, not nearly enough physics. Sorry

 

[haruspex]

So M1_iV_o = M1V1_fCos(theta)+M2V2_fcos(phi)+M1V1_f-M2V2_fsin(phi)

you seem to have a basic misapprehension regarding momentum.
Momentum is a vector, and your 'relevant equation' for its conservation should be interpreted in that light.
When resolving into separate X and Y directions, that gives you two momentum conservation equations, one for each direction. But you appear to have collapsed them into one scalar equation.

 

[-PhysicsMajor-]

you seem to have a basic misapprehension regarding momentum.
Momentum is a vector, and your 'relevant equation' for its conservation should be interpreted in that light.
When resolving into separate X and Y directions, that gives you two momentum conservation equations, one for each direction. But you appear to have collapsed them into one scalar equation.

Thank you for bringing this up, because it seemed wrong when I was doing it. I guess I just got confused because there is no inital momentum in the y direction.

So
P_ix=P_fx = M1iVo = M1V1fCos(theta)+M2V2fcos(phi)
P_iy = P_fy = 0 = M1V1fsin(theta)-M2V2fsin(phi)

??

 

[haruspex]

Thank you for bringing this up, because it seemed wrong when I was doing it. I guess I just got confused because there is no inital momentum in the y direction.

So
P_ix=P_fx = M1iVo = M1V1fCos(theta)+M2V2fcos(phi)
P_iy = P_fy = 0 = M1V1fsin(theta)-M2V2fsin(phi)

??

Yes.