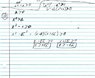Again, it would be helpful if you posted your work directly on this page rather than a screen shot. As already mentioned, anyone helping needs to keep track of two screens. For another thing, to comment on your work, I have to type it, too, in addition to comments I make.
If you want help, don't make it more difficult for someone to give you help.
In the work you posted, there are several things that aren't true.
You wrote 0 <= |a|. This is true by definition. Your reason is incorrect, though.
"because a must be a positive value" - a can be any real number. |a| can be either 0 or positive, but it can't be negative.
"if absolute value of a is on the negative side ..." - |a| is never negative.
"if it is on the positive side the (sic) a is = to a" -- Any number is always equal to itself. What's the point of saying this?