ricky_fusion
- 22
- 0
Hi..
I've got a problem about moment inertia. I don't understand about looking the distance of centroid (y). I am still confucing about the formula of "y" in Moment Inertia. Can you shows me about the formula of y or if any thread for this before, I am glad to see it too.Thanx's for your help..
I still don't know how to find put y =30 and 35
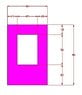
Known : You can see the dimension and the picture in my attachment
Asking: How is to calculate y ?? Is the formula same to all geometry??
I = y dA
Cross section
Total Area: - A =>40*60=2400
- y => 30 Why is it 30?
- Ay =>72000
Inside Area:-A=> -20*30=-600
-y =>35 Why is it 35?
- Ay => -21000
I've got a problem about moment inertia. I don't understand about looking the distance of centroid (y). I am still confucing about the formula of "y" in Moment Inertia. Can you shows me about the formula of y or if any thread for this before, I am glad to see it too.Thanx's for your help..
I still don't know how to find put y =30 and 35
Homework Statement
Known : You can see the dimension and the picture in my attachment
Asking: How is to calculate y ?? Is the formula same to all geometry??
Homework Equations
I = y dA
The Attempt at a Solution
Cross section
Total Area: - A =>40*60=2400
- y => 30 Why is it 30?
- Ay =>72000
Inside Area:-A=> -20*30=-600
-y =>35 Why is it 35?
- Ay => -21000