Inertia of System: Find w/ Pink Dot & Diagonals

AI Thread Summary
The discussion focuses on calculating the inertia of a system with a rotation axis through the center of mass, indicated by a pink dot. The user initially believes the radius (r) should be the square root of 13, but is corrected that r represents the perpendicular distance from the mass to the axis of rotation, which is 3 (half of 6). This clarification emphasizes the importance of understanding the definition of r in relation to the axis of rotation. The conversation highlights the need to review definitions and concepts related to rotational dynamics. Accurate interpretation of these concepts is crucial for solving inertia problems effectively.
Hanin
Messages
1
Reaction score
0
Member advised to use the provided formatting template when starting a new thread in a homework forum.
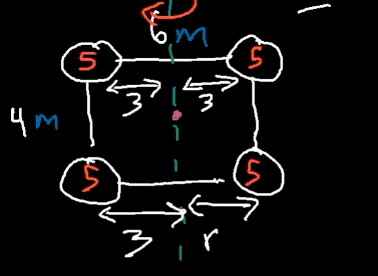
Hi, in the following problem, I need to find the inertia of the system. The axis of rotation passes through the center of mass ( the pink dot). I understand that I will be equal to 4(mr^2). However, I do not understand why r= 3 (6 divided by 2) and not sqrt13 ( half of the diagonal of the rectangle).

upload_2017-12-8_20-27-53.png

 

Attachments

  • upload_2017-12-8_20-27-53.png
    upload_2017-12-8_20-27-53.png
    7.7 KB · Views: 451
Physics news on Phys.org
Review your definitions. r is the perpendicular distance from the mass to the axis of rotation, which is that entire line through the center, not the distance from the mass to the point in the center.
 
  • Like
Likes Abhishek kumar and Hanin
I think you were thinking rotation about the c.g. into/out of page.
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Moment of inertia of a cuboid parallel to one of its faces (repost with diagram)
Replies
25
Views
2K
What is the "r" in the moment of inertia?
Replies
13
Views
2K
Rotational Inertia: Hoop vs Disk
Replies
19
Views
3K
How Does Angular Momentum Conservation Affect Asteroid Collision Dynamics?
7
Replies
335
Views
13K
Rolling without slipping problem
Replies
42
Views
3K
Determining $L_{o}$: Finding Angular Momentum of System
Replies
45
Views
4K
Why can we use this approximation in rotational work-kinetic energy theorem for small displacements?
Replies
7
Views
1K
Finding the Moment of Inertia for a Rectangular Sheet
Replies
1
Views
4K
System of two wheels of different sizes with an axle through their centers
2
Replies
67
Views
4K
How Does Adding Masses Affect the Angular Velocity of a Rotating Cylinder?
Replies
12
Views
3K

Hot Threads

Recent Insights

Back
Top