Initial acceleration of a projectile incl air resistance

[mitch_1211]

Homework Statement

Conditions: (ii)x0 =0 and v0 =20ms−1
with a mass of 1 kg with c1 = 0.2kgs−1 and c2 = 0.02kgm−1

projectile is fired directly up (only considering motion in the EDIT y direction (previously x by mistake)) at 20m/s
given eqn can calculate acceleration at the n+1 term (i.e 1 second or 0.2 seconds etc, whatever is chosen for delta t) but I can't get it to work for the initial acceleration. In part 1, the projectile was freefalling (beginning at v=0 )so acceleration was just that of gravity (9.81m/s/s). I know that this time it will be gravity as well as some air resistance (drag) terms. The eqn attached gives those terms, but only for the n+1 term, i.e the next acceleration term. I can't get this to work for the initial conditions.

have defined gravity to be working in the neg direction, all things going up are positive and down are negative

Homework Equations

see attached image for eqns for position, velocity and acceleration

The Attempt at a Solution

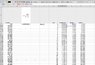
i'm using a spreadsheet so as to organise my data quickly. I can get some values for acceleration, will also attach screen shot of the columns i used. My velocity reaches a terminal velocity instead of getting lower and lower. consequently the projectile never stops and never reaches the max height of its trajectory.

for used in spreadsheet for each n+1 term in acceleration;
=(($B$9)-(($B$10*S3)+($B$11*S3*(ABS(S3)))))

b9 is accl due to gravity = 9.81 (no neg sign is in the cell)
b10 is c1=0.2
b11 is c2=0.02
s3 can be seen from attached image (ignore what is on the left of the image, it is part 1, I'm working on case 2)

thanks!
Mitch

Homework Statement

Homework Equations

The Attempt at a Solution

 

[mitch_1211]

have since solved this problem. turns out using 0.2seconds for delta t makes the formula calculate too large a step (the motion only lasts 3 seconds) choosing delta t to be 0.01 seconds solved my problem