Joshua Benabou
Consider a parallel plate capacitor formed by two plates of length ##L## and width ##d##, separated by a distance ##e##. There is a vacuum in between the plates. Let's note the capacitance of this arrangement ##C_0##.
I insert a conducting plate of length ##l=L/2##, with ##D##, and thickness ##e' <<e##. The position of the plate is measured by its ##(x,y)## coordinates, as shown below:
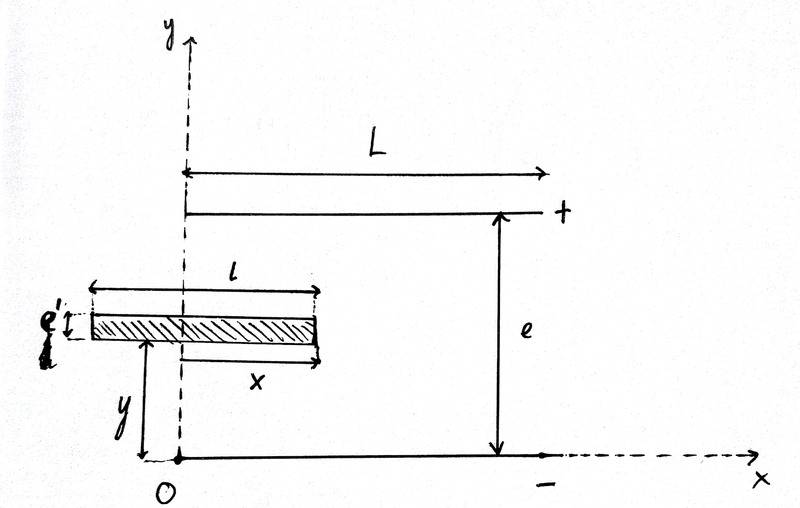
I would like to find the equivalent capacitance of this apparatus in terms of the distance ##x##.
Of course if ##x<0##, the conductor is not inserted at all so the capacitance remains unchanged, ##C_0##.
Consider the case where the conductor is inserted partially, i.e ##0<x<l##.
According to my notes, in this case the apparatus is equivalent to the arrangement of capacitors below:
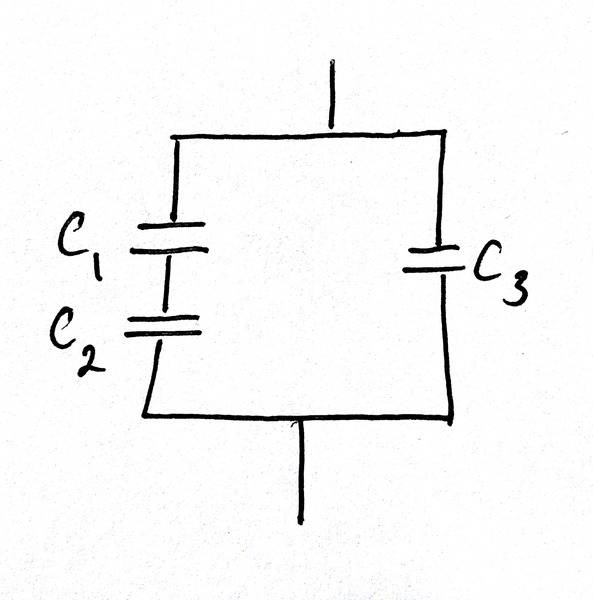
where
##C_1=\frac{\epsilon_0Dx}{e-y-e'}##
##C_2=\frac{\epsilon_0Dx}{y}##
##C_3=\frac{\epsilon_0D(L-x)}{e}##
**I do not understand why this configuration is equivalent to the arrangement of capacitors given above.**
I guess ##C_1## is the capacitor formed by the top plate and the conductor, ##C_2## the capacitor formed by the bottom plate and the conductor, and ##C_3## the capacitor formed by the conductor itself. However this leaves me confused as the capacitance for the conductor should then be:
##C_3=\frac{\epsilon_0Dx}{e}##
Finally, if we now consider the case where the conductor is fully inserted, i.e ##l<x<L##, then apparently the capacitor arrangement changes completely and we now actually have four capacitors (2 in series, which are parallel with the other two). I don't understand why.
I insert a conducting plate of length ##l=L/2##, with ##D##, and thickness ##e' <<e##. The position of the plate is measured by its ##(x,y)## coordinates, as shown below:
I would like to find the equivalent capacitance of this apparatus in terms of the distance ##x##.
Of course if ##x<0##, the conductor is not inserted at all so the capacitance remains unchanged, ##C_0##.
Consider the case where the conductor is inserted partially, i.e ##0<x<l##.
According to my notes, in this case the apparatus is equivalent to the arrangement of capacitors below:
where
##C_1=\frac{\epsilon_0Dx}{e-y-e'}##
##C_2=\frac{\epsilon_0Dx}{y}##
##C_3=\frac{\epsilon_0D(L-x)}{e}##
**I do not understand why this configuration is equivalent to the arrangement of capacitors given above.**
I guess ##C_1## is the capacitor formed by the top plate and the conductor, ##C_2## the capacitor formed by the bottom plate and the conductor, and ##C_3## the capacitor formed by the conductor itself. However this leaves me confused as the capacitance for the conductor should then be:
##C_3=\frac{\epsilon_0Dx}{e}##
Finally, if we now consider the case where the conductor is fully inserted, i.e ##l<x<L##, then apparently the capacitor arrangement changes completely and we now actually have four capacitors (2 in series, which are parallel with the other two). I don't understand why.