Insight/Intuition into rotations in R²

[STENDEC]

I've been using rotation matrices for quite some time now without fully grasping them. Whenever I tried to develop an intuitive understanding of...<br /> x&#039; = x\cos\theta - y\sin\theta \\<br /> y&#039; = x\sin\theta + y \cos\theta<br />... I failed and gave up. I've looked at numerous online texts and videos, but following the step-by-step explanations didn't lead to me seeing the whole picture as I had hoped.

Could someone explain to me (like I'm 5 years old), why -y\sin\theta and x\sin\theta are used to affect the value along the other axis?

Looking at the following picture (pardon the quality):

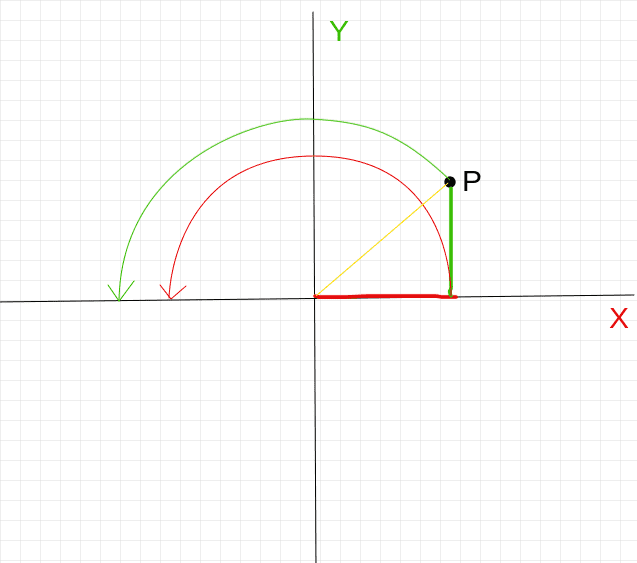
Is the contribution of y to x and vice versa there, to ensure that P maintains the correct distance to the origin, or is that a misguided simplification of mine? The yellow line cannot be sin + cos (Pythagorean theorem) yet I may combine these two to get x&#039; and y&#039;. Do you see where my gap in understanding lies? Is there a drawing that could clarify how these terms combine to give the correct value we observe? Algebraic proofs don't work with me I'm afraid, I need a geometric/visual explanation.

 

[jedishrfu]

MAYBE THIS VIDEO WILL HELP:

 

[Edgardo]

Here is a good explanation:
http://mathforum.org/library/drmath/view/74063.html

 

[suremarc]

The component $\left(\begin{smallmatrix}x\cos\theta\\y\cos\theta\end{smallmatrix}\right)$ represents the projection of $\left(\begin{smallmatrix}x'\\y'\end{smallmatrix}\right)$ onto the original vector $\left(\begin{smallmatrix}x\\y\end{smallmatrix}\right)$. The other component (the "rejection") should therefore have magnitude $|\sqrt{x^2+y^2}\sin\theta|$ and be orthogonal to the projection. There are two unique solutions for such a vector.

Finally, when $\theta$ is nonzero but less than a straight angle, an increase in $y'$ corresponds to a decrease in $x'$; i.e., the x-component of the rejection should be negative. (This condition is equivalent to a choice of orientation on $\mathbb{R}^2$.) This tells us which solution is the desired one.

As for your drawing, I don't quite understand what you mean. Could you elaborate?