smashbrohamme
- 97
- 1
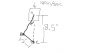
The figure below shows the piston-cylinder-crank arrangement in an internal combustion engine. When the piston is in the position shown in the figure, it has a downward speed of 900ft/min.
I converted the 900ft/min to 180in/sec.
I did the whole problem but I realized I used the wrong length on link AB.
I used the 8.5in length for AB but I still encountered a problem on solving this problem with the vectors.
The three questions to answer are.
A. Find the Angular Velocity of link AB
B. Find the velocity of point B on the crank.
C. Find the Angular Velocity of Crank BC.
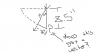
Now the vectors I have are shown in the next attachment, is this right?
Also everytime I try to solve for length AB i get some weird answer, shouldn't this be a simple LAW of SINES problem? I keep getting 9.5inches, which just doesn't make any sense at all.
Please help I just got off spring break and my mind is jumbled with pizza and video games lol.
I converted the 900ft/min to 180in/sec.
I did the whole problem but I realized I used the wrong length on link AB.
I used the 8.5in length for AB but I still encountered a problem on solving this problem with the vectors.
The three questions to answer are.
A. Find the Angular Velocity of link AB
B. Find the velocity of point B on the crank.
C. Find the Angular Velocity of Crank BC.
Now the vectors I have are shown in the next attachment, is this right?
Also everytime I try to solve for length AB i get some weird answer, shouldn't this be a simple LAW of SINES problem? I keep getting 9.5inches, which just doesn't make any sense at all.
Please help I just got off spring break and my mind is jumbled with pizza and video games lol.