- #1
Winzer
- 598
- 0
Homework Statement
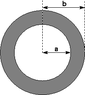
A long cylindrical insulating shell has an inner radius of a = 1.38 m and an outer radius of b = 1.61 m. The shell has a constant charge density of 4.80 C/m3.1. What is the magnitude of the electric field at a distance of 1.87 m from the axis?
2. What is the magnitude of the electric field at a distance of 1.51 m from the axis?
3. If we take the potential at the axis to be zero, what is the electric potential at the outer radius of the shell?
Homework Equations
[tex] E=\frac{kq}{r^2}[/tex]
[tex] \oint \vec{E}\vec{dr}= \frac{Q_{Enclosed}}{\epsilon_{o}}[/tex]
The Attempt at a Solution
For 1 i use [tex] E=\frac{kq}{r^2}[/tex] but i am confused on finding q because i am given density of c/m^3. I am assuming an infinity long cyclinder?[tex]\vec{}[/tex]