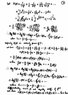mathslover
- 17
- 0
Hi guys,recently I came across the following integral and need assistance in solving the problem.
The crux of the problem is calculating the definite integral of log(sin(x)*sin(x)) over
the interval ( 0, Pi/2).
Sorry, I made a mistake in typing the integrand.
It should be (Log(sin(x)))^2 instead.
The crux of the problem is calculating the definite integral of log(sin(x)*sin(x)) over
the interval ( 0, Pi/2).
Sorry, I made a mistake in typing the integrand.
It should be (Log(sin(x)))^2 instead.
Last edited: