Integral for Current through an Inductor -- Not Working

[Lapse]

Homework Statement

[/B]
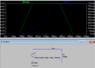
Calculate, and plot along with (on the same plot) the voltage seen below, the current flowing in the following circuit using the integral relationship between the voltage across an inductor and the current through the inductor. Verify your hand calculations and plot using LTspice.

Homework Equations

I = I_o+1/L ⋅ ∫Vdτ

The Attempt at a Solution

So I am obviously doing this incorrectly because the current I obtain from solving the integral doesn't match the graph. For example, If I want the current from time 100μs - 200μs:

I = 0 + 1/400μH∫1dτ = 250mA

250mA is too high according to the graph. Where am I going wrong here?

 

[vela]

Why are you integrating a constant when the voltage across the inductor isn't constant over that time interval?

 

[Lapse]

Good question. So what equation do I use to figure the current through the inductor?

 

[gneill]

You need to break up the voltage vs time equation into piecewise continuous sections and integrate over each piece.

 

[DaveE]

You have the correct equation, you just need to do the integral correctly. It may help to think of finding the "area" (volts*sec) under the voltage curve.