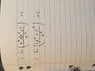DJ-Math
- 4
- 0
Member warned about posting with no template and no effort shown
Hi,
I'm trying to solve ∫(x2-1)/(1+x2)*1/(1+x4)(1/2)dx
I'm apparently meant to get some non-complex result, the question suggests to use the substitution u2 = x2 + 1/x2
But I haven't gotten anywhere with this.
Any methods or suggestions (or the solution) would be much appreciated!
Thanks
I'm trying to solve ∫(x2-1)/(1+x2)*1/(1+x4)(1/2)dx
I'm apparently meant to get some non-complex result, the question suggests to use the substitution u2 = x2 + 1/x2
But I haven't gotten anywhere with this.
Any methods or suggestions (or the solution) would be much appreciated!
Thanks