omonoid
- 18
- 0
Integral of cos(8x^2)? multivariable calc
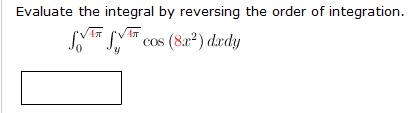
none
So i reversed the order...
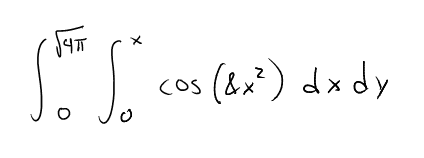
and couldn't figure out how to integrate cos(8x^2). I looked at my trig identities, tried on my graphing calc, and even wolfram alpha gave me a strange answer that i can't use.
Either I'm doing something wrong, or missing something obvious.
Thanks
Jake
Homework Statement
Homework Equations
none
The Attempt at a Solution
So i reversed the order...
and couldn't figure out how to integrate cos(8x^2). I looked at my trig identities, tried on my graphing calc, and even wolfram alpha gave me a strange answer that i can't use.
Either I'm doing something wrong, or missing something obvious.
Thanks
Jake