Karol
- 1,380
- 22
Homework Statement
A stone falls from a high tower. what is the distance, in the x direction, parallel to the ground, that the stone reaches, caused only by the x component, the tangential component, of the gravity, after t seconds of free fall.
Homework Equations
The constant acceleration formula:
x=\frac{1}{2}a\cdot t^2
The Attempt at a Solution
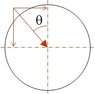
According to the drawing attached, the acceleration in the x direction is:
a=g\cdot\sin\theta=g\sin(\omega t)
Where ω is the angular velocity of the earth.
I insert this a into the constant acceleration formula, since i don't know anything else, and, maybe, in short intervals of time the acceleration is approximately constant.
So, i get:
dx=\frac{1}{2}g\sin(\omega dt)\cdot dt^2
And:
x=\frac{g}{2}\int_{0}^{4} \sin(\omega t)\cdot t^2
Is this approach correct? since, numerically, the results aren't.
 . The tower height is not needed. My h above should be the vertical distance fallen in time t, so it reduces to ωgt3 sin(θ)/2 = 2.3 cm at the equator.
. The tower height is not needed. My h above should be the vertical distance fallen in time t, so it reduces to ωgt3 sin(θ)/2 = 2.3 cm at the equator.