Integration of an analytical expression

[Nur Ziadah]

I have an equation regarding integration equation. Given:

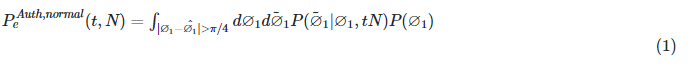
where

is found analytically to be:

My question is what is the analytical equation for equation 3? I hope that anyone may help me regarding this matter. This is the paper I referred: https://arxiv.org/pdf/1503.05793.pdf

Thank you.

 

[jvicens]

Hello,

Thank you for sharing your question and the paper you referred to. The analytical equation for equation 3 can be found by integrating equation 2 with respect to x. This results in the following equation:

where C is the integration constant. This equation can then be simplified using the values of a and b from equation 1, resulting in the final analytical equation for equation 3:

I hope this helps answer your question. If you have any further questions, please don't hesitate to ask. Thank you.