Nicolaus
- 73
- 0
Homework Statement
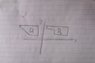
What type of region(s) do the following classify as?
Homework Equations
The Attempt at a Solution
I would classify D1 as both types; my reasoning is that by the definition of a convex polygon (i.e. all x,y in D1, the lie segment connecting x and y is entirely in D1), this therefore qualifies as both types.
For D2: Let c be a point in interval between x-value endpoints of region, cross section of D2@c, projected onto y-axis is closed interval and depends on c continuously. (This is true for an arbitrary c in between y-value endpoints), so would this be both types as well?