Integration to volume and Demoivre's Theorem

[jackscholar]

Homework Statement

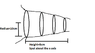
1)I need to find the volume of the shape attached.
2) Solve cos5θ in terms of cos only.

The Attempt at a Solution

1) I believe the shape is a cylinder that has a radius which decreases with height. Does this mean i integrate the volume of a cylinder in the equation:
V=∏∫y^2 dh where y represents the first circles radius of 10cm, and the limits of integration are 5 and 0 for the upper and lower bounds respectively?
2) My teacher has told me to use demoivre's theorem such that, cos5θ=(cosθ+isinθ)^5, and this is expanded using binomial distribution. From here any terms that contain an imaginary number are eliminated from the equation? I'm not sure if they are right and I'm even more confused as to where to go from there.

Any help is highly appreciated!

 

[lippyka]

1) Yes, you are correct. The volume of the shape is given by V=π∫y2dh, where y is the radius of the cylinder which decreases with height, and the limits of integration are 5 and 0 for the upper and lower bounds respectively. So, the volume of the shape is given by V=π∫10-h2dh, where h is the height of the cylinder. 2) Yes, you are correct. Using De Moivre's theorem, cos5θ=(cosθ+isinθ)^5, and this is expanded using binomial distribution. Then eliminate any terms that contain an imaginary number. This leaves us with the equation cos5θ = cos5θ + 5cos4θsinθ - 10cos3θsin2θ + 10cos2θsin3θ - 5cosθsin4θ + sin5θ Finally, since we want the answer in terms of cos only, we can set sinθ = 0, which gives cos5θ = cos5θ + 5cos4θ(0) - 10cos3θ(0) + 10cos2θ(0) - 5cosθ(0) + (0) Hence, cos5θ = cos5θ.